タイヤモデル
タイヤモデルについては以下をご覧ください.
Magic Formulaとは
Magic Formulaは1980年代半ばに,ボルボのBakkerらとデレフト工科大学のPacejkaらによって共同で開発されました.Magic Formulaは,4つの変数 とスリップ率・スリップ角を入力として,タイヤの力またはトルクを出力とするタイヤモデルであり,それらの入出力関係は三角関数(逆三角関数)を用いて表されます.この式をここでは基礎式と呼びます.さらに,その4つの変数
はを他の入力(空気圧や輪荷重など)と10-20程度の係数との線形和で表されます.(詳しくは後述します. )そして,タイヤの試験データを用いてそれらの係数を同定する事により,関数が一意に決まります.それに加え,晴れや雨などの条件に対応できるよう,倍率係数という変数も用意されています.
Magic Formulaには,ピュアモデルとコンバインドモデルの2種類があります.ピュアモデルは単一方向(縦または横)の試験データのみを用いたタイヤモデルで,試験が少なく済みますが適用範囲が絞られてしまいます.コンバインドモデルは縦横両方の試験データを活用し,摩擦円を考慮したタイヤモデルとなります.ABSなどのシステムの発展によって,コンバインドモデルの需要がかなり高まっています.
基礎式
Magic Formulaの基礎式はバージョンや入出力によらずに一つの式によって表されます.
with
ここで, は入力である
(スリップ角)または
(スリップ率)を表し,
は出力である横力,縦力またはセルフアライニングトルクを表します.
基礎式に現れる変数はそれぞれ,剛性係数
,形状係数
,ピーク値
,曲線係数
,水平方向シフト
,垂直方向シフト
と呼ばれます.
これらの係数(ここでは便宜上,上級係数と呼ぶ)は,さらにスリップ角・スリップ率以外の入力(空気圧・輪荷重・キャンバ角など)とより細かい係数(下級係数と呼ぶ)によって表されます. この下級係数による上級係数の表現方法はMagic Formulaのバージョンによって異なります.より沢山の下級係数を用いて複雑な式を用いて表現すれば,より正確なタイヤモデルを得られるように思えますが,実際は過学習の問題や局所最適解にはまってしまって最適解を得られないといった問題が生じるため,十数~数十個の係数を用いる場合が多いです.(しかし,近年の深層学習の発展によって,多くの係数(パラメータ)を用いて同定する方法も提案されています.)
各係数の特徴
剛性係数
式を見れば分かるように全てが の前に付きます.つまり,
方向に拡大縮小をする役割があります.
 の積
の積
基礎式を微分すれば分かりますが,原点での傾きは になります.
ピーク値 
正弦関数の最大値は1であるので, がピーク値になります.
形状係数 
と
の意味からも推測がつくように
は形状を表します.
曲率係数 
曲線のピーク付近の曲率に影響を与えます. は
に依存して変化します.
シフト値 
タイヤ各々の不均一性によります. はconicityに,
はply steerによると言われます.
より細かい係数(分かりやすいよう下級係数と呼んでいます)について
下級係数はスリップ率・スリップ角以外の入力(空気圧・輪荷重・キャンバ角など)との線形結合によって上級係数を表現します.このように定数が2階層に分かれているのですが,このように分けられたのは恐らく表現が完結にまとめられて,かつ係数を同定しやすくなるというのが2階層に分けられた理由なんじゃないでしょうか.(実際に2階層に分けたことで同定がしやすい場合が多く,そのような同定法を2段同定法と呼ぶそうです[水野ら1999].
上述したように,下級係数の定義はバージョンによって異なります.現状一般的なモデルは,MF-Tyre 6.1というタイヤモデルです.PacejkaによるTyre and Vehicle Dynamics 3rd eddition内に掲載されています.
基礎式の解析
Magic Formulaの基礎式は
という形で表されるわけですが,どうしてこのような形を取るのでしょうか?
実験に得られる横力のタイヤデータは以下の図の青線のような形です.
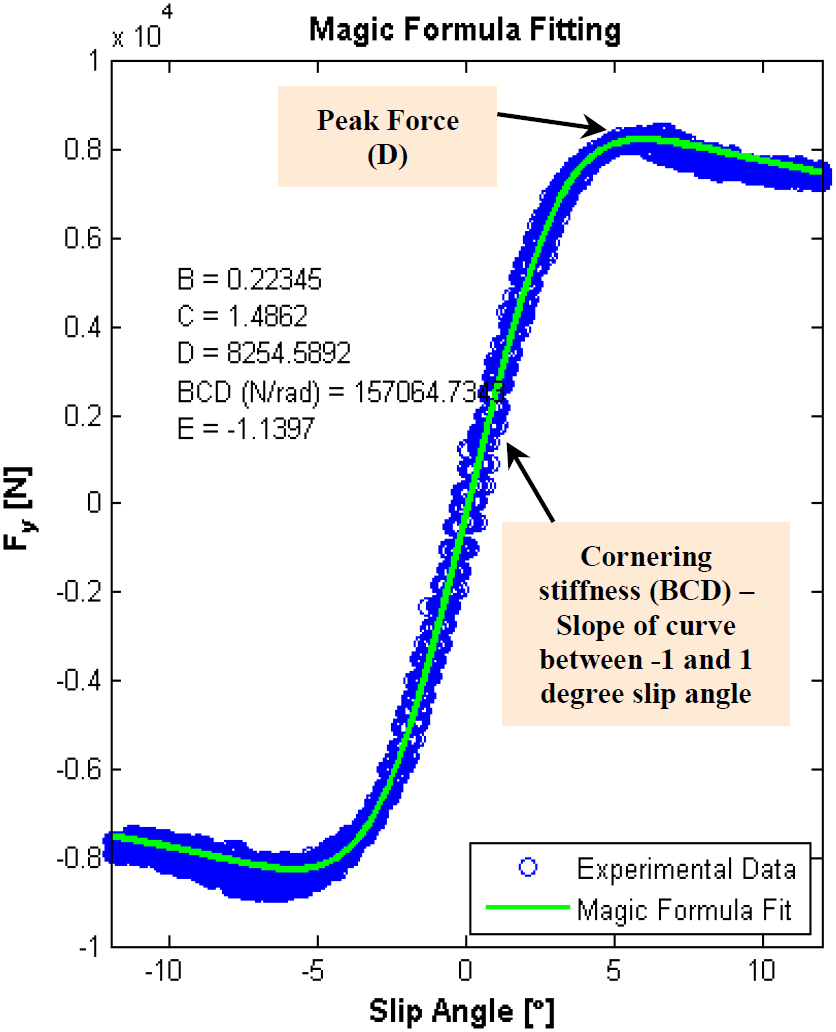
おおよそ 関数の区間
くらいを区間
まで引き伸ばしたような形をしています.なので,ある関数
を用いて
とすれば,「
関数の区間
を区間
まで引き伸ばした」関数を構築することができます.さて,そのような関数
をあなたはご存知でしょうか.そうです.
です.
は実数空間
を
に写します.なので,
を定義して,
とすることで,先ほどの「
関数の区間
を区間
まで引き伸ばした」関数を書くことができます.この
は基礎式の形状係数
です.名前の由来も理解できたのではないでしょうか.
次に, 関数の最大値は1であるのに対して,タイヤデータの最大値は数万Nと非常に大きいので,タイヤデータの最大値を
として(実際は少し違います),
と書きます.これがピーク値
です.
そして, によって縦軸方向のスケールを合わせたのと同様に,横軸方向のスケールを
によって調整できるようにします.すなわち,
と書きます.
あとは, の部分です.
については既に述べたので,簡単のために
として,
について見ていきます.これは,
のマクローリン展開を用いて近似することでおおよそ理解できます.
のマクローリン展開は
と表され, に適用すると,
と展開できます.なので, は
に対する高次の項の影響を調整するための係数になっています.これはつまり,
が小さい時は
の値は
の影響を大きく受け,
が大きい時は高次の項の影響を大きく受けるということなので,
は原点から遠い位置での曲線の形に影響します.よって,
は曲率係数と呼ばれます.(なぜここで
を用いたのかについては,現状私は理解できていません.ご存知の方,ご教授いただければ幸いです.)
各係数をおおよそ同定してみる
 について
について
タイヤ発生力の最大値からおおよそ求まります.
 について
について
で
なので,
でのタイヤの発生する力を
とすれば,
となり,これを式変形すれば
と が求まります.
 について
について
傾きから がわかり,上述から
がわかるので,求まります.
 について
について
が最大となる
を
とすると,その時
の中身は
となるので,
となります.式変形をして は以下になります.
参考文献
Singh, Kanwar & Sivaramakrishnan, Srikanth. (2015). An adaptive tire model for enhanced vehicle control systems. SAE International Journal of Passenger Cars - Mechanical Systems. 8. 10.4271/2015-01-1521.
